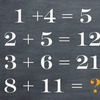U pravilu bi nam za rješenje sustava jednadžbi s tri nepoznanice trebale tri jednadžbe. No, nekad je dovoljna i samo jedna
Matematika je kao kraljica znanosti bezrazložno ozloglašena. U krajnjoj liniji zato što se svaki problem da jednostavno i ljudski objasniti. Pojedinci se, međutim, i u odrasloj dobi znaju sjećati trauma koje su imali tijekom satova matematike, posebno ako im nastavnik ili nastavnica nije posjedovao sretan omjer vještine objašnjavanja i strogoće ispitivanja.
Ovaj je članak dio naše pretplatničke ponude.
Cjelokupni sadržaj dostupan je isključivo pretplatnicima.
S pretplatom dobivate neograničen pristup svim našim arhiviranim člancima,
ekskluzivnim intervjuima i stručnim analizama.